Contents

Open In Colab

基本的な統計量とガウス分布

要約統計量の概要

  • 要約統計量とは、標本の分布の特徴を代表的に（要約して）表す統計学上の値であり、統計量の一種

    • 主にデータの分布の中心や拡がりなどを表わす

    • 基本統計量、記述統計量、代表値とも呼ばれる

以下は、要約統計量の例

  1. モーメントから求められる要約統計量

  • 平均

  • 分散、標準偏差

  • 歪度

  • 尖度

  1. 順序から求められる要約統計量

  • 中央値

  • 刈込平均（トリム平均）

  • 四分位点

  • 最小値・最大値

  • 中点値

  • 範囲

  1. 度数から求められる要約統計量

  • 最頻値

モーメントから求められる要約統計量

N 個のデータ \(x_1,\ x_2,\ \dots,\ x_N\) に対する統計量を考える。まず、平均値 \(\mu\) と、平均値まわりの m 次中央モーメント[1] \(\mu_m\) を

\[\mu = \frac{1}{\,N\,} \sum_{i = 1}^N x_i\]
\[\mu_m = \frac{1}{\,N\,} \sum_{i = 1}^N (x_i - \mu)^m \quad\ (m = 2, 3, \cdots)\]

で定義する。

平均

原点まわりの1次モーメント \(\mu\)。和を個数で割ったもの。

\[\mu = \frac{1}{\,N\,} \sum_{i = 1}^N x_i\]

分散、標準偏差

2次中央モーメントから求められる統計量。分布の広がりを表す。

分散：　　 \(\sigma^2 = \mu_2\)
標準偏差： \(\sigma = \sqrt{\mu_2}\)

歪度

3次中央モーメントから求められる統計量。分布の左右非対称の度合いを表す。

\(\gamma_1 = \mu_3 / \sigma^3\)

尖度

4次中央モーメントから求められる統計量。分布の峰の鋭さ（裾野の広さ）を表す。

\(\gamma_2 = \mu_4 / \sigma^4 - 3\)

ただし、3 を引かない定義もある。

[1]: 用語 「m 次中央モーメント」は、竹内啓（編集委員代表）『統計学辞典』東洋経済新報社, 1989 による。

順序から求められる要約統計量

以下、昇順にソートされた N 個のデータ \(x_1 \le x_2 \le \dots \le x_N\) に対する統計量（順序統計量）を考える。

中央値

メジアン、メディアン (median) ともいう。データの大きさに関してちょうど中央に当たるデータ \(x_{(N+1)/2}\) 。ただし、整数でない添数に対する中央値は線形補間によって定義する（つまり N が偶数のときは \(x_{N/2}\) と \(x_{(N+1)/2}\) の平均とする）。

刈込平均（トリム平均）

最大値、最小値を除外した平均。除外する数を増やして行くと、最後は中央値になる。そのため、中央値は刈込平均の一つである1。

四分位点

集団を値の大きさで4等分するとき、その境界となる値。\(x_{(N+3)/4}\) を第1四分位点、\(x_{(3N+1)/4}\) を第3四分位点という。\(x_{(2N+2)/4}\) 、つまり第2四分位点は中央値である。

最小値・最大値

集団に含まれる最も小さい値 \(x_1\) と、最も大きい値 \(x_N\) 。

これらの統計量を視覚化するために、箱ひげ図を用いる。

中点値

最大値と最小値を足して2で割ったものを中点値とよび、代表値として用いることがある。

範囲

最大値と最小値の差を範囲(range)とよび、代表値として用いることがある。記号はRを用いる。

度数から求められる要約統計量

最頻値

モード (mode)、並み数 ともいう。データのうち、度数分布において最も高い度数を示す値、つまり最も多く現れているデータの値。

不偏分散 (unbiased estimator of varianc)

\[u^2 = \frac{1}{N-1} \sum_{i = 1}^N (x_i - \mu)^2 \quad\ \]

不偏分散 \(u^2\)

通常母集団の分散は通常の 分散を、標本から母集団の分散を推測する場合は不偏分散を使う。 Excel 関数の var() は不偏分散を計算する。

機械学習の分野では、不偏分散ではなく、上記で説明した分散を使うことが多い。 （どちらを用いたとしても、似た結果を得ることができ、ほとんど同じ解釈をすることができる）

参考：https://www.heisei-u.ac.jp/ba/fukui/pdf/stattext05.pdf

IRISデータを使って要約統計量を求めてみる

  • IRISデータとは？

機械学習で有名なデータ． IRISは「あやめ」の花を意味しており，UCI（カリフォルニア大学アーバイン校）から機械学習やデータマイニングの検討用データとして配布されている．

あやめの種類は以下のとおり．

  • セトナ(setosa)

  • バーシクル(versicolor)

  • バージニカ(virginica)

このデータを以下の情報から分析する．

  • がく片長(Sepal Length)

  • がく片幅(Sepal Width)

  • 花びら長(Petal Length)

  • 花びら幅(Petal Width)

単位は、いずれも cm。

image01

https://carp.cc.it-hiroshima.ac.jp/~tateyama/Lecture/AppEx/LoadCSV.html

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
from sklearn import datasets

iris = datasets.load_iris()
iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
iris_df['name'] = iris.target_names[iris.target]

# pandas で簡単に、主要な統計量を出力できる。
# もちろん、それぞれ個別に出力することもできるがここでは省略。
iris_df.describe()
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
count 150.000000 150.000000 150.000000 150.000000
mean 5.843333 3.057333 3.758000 1.199333
std 0.828066 0.435866 1.765298 0.762238
min 4.300000 2.000000 1.000000 0.100000
25% 5.100000 2.800000 1.600000 0.300000
50% 5.800000 3.000000 4.350000 1.300000
75% 6.400000 3.300000 5.100000 1.800000
max 7.900000 4.400000 6.900000 2.500000 
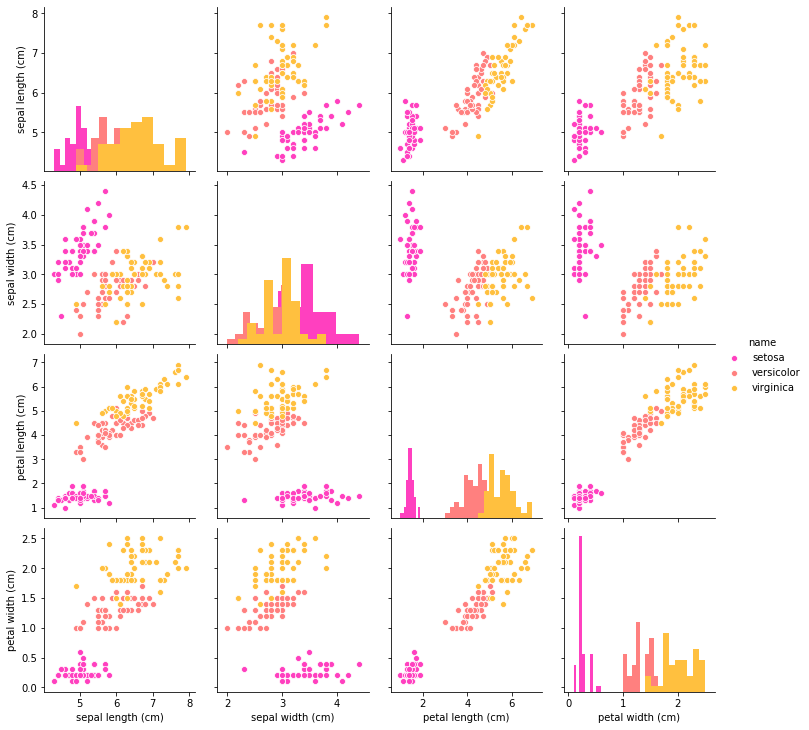
# データの確認
plt.show(sns.pairplot(data=iris_df, hue='name', vars=iris.feature_names, diag_kind='hist', palette='spring'))
../_images/basic_statistic_values_11_0.png

共分散 (Covariance)

1つの標本が、2つ以上の特徴量を持つとき、特徴量1、 \(x^{\left( 1\right) }\) 、と特徴量2、 \(x^{\left( 2\right) }\) 、の間の共分散は、以下のように表す。

\[ cov(x^{\left( 1\right) }, x^{\left( 2\right) }) = \frac{1}{N} \sum_{i = 1}^N (x^{\left( 1\right) }_{i} - \mu^{\left( 1\right) }) (x^{\left( 2\right) }_{i} - \mu^{\left( 2\right) }) \quad \]

2つの特徴量の間に、正の相関がある場合は正の値、負の相関がある場合は負の値をとる。値の大きさが相関の強さを表す。 ただし、これは、2つの特徴量の単位（尺度）が同じ場合のみである。

共分散（行列）は、次回 (?) 紹介する、主成分解析（PCA analysis）で使う。

https://ja.wikipedia.org/wiki/共分散

分散共分散行列（共分散行列、Variance-covariance matrix、Covariance matrix）

次のような列ベクトルを考える。 \(X_1, X_2, ... , X_m\) は、異なる m 個の特徴量を表す。

\(\textbf{X}= \begin{bmatrix}X_1 \\ X_2 \\ \vdots \\ X_m \end{bmatrix}\)

このベクトルの要素が各々分散が有限である確率変数であるとき、( ‘’i’’, ‘’j’’ ) の要素が次のような行列 Σ を分散共分散行列という。

\[\Sigma_{ij} = \frac{1}{N} \sum_{i = 1}^m (X_{i} - \mu_{i}) (X_{j} - \mu_{j}) \quad\ \]

N は標本の数である。 つまり、対角成分は分散、それ以外は共分散となる行列を分散共分散行列という。

特徴量のすべてのペアの共分散を見ることができる。

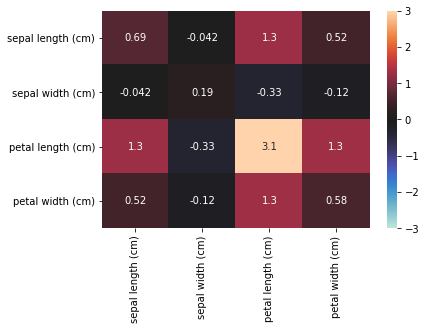
以下に、iris データセットの各特徴量の分散共分散行列をヒートマップで示す。
対角成分が分散、それ以外の成分が共分散となっている。
例えば、petal length と sepal length に正の相関があることがわかる。

import numpy as np

# 共分散行列を作成
cov_mat = np.cov(iris.data.T)
df = pd.DataFrame(cov_mat, index=iris.feature_names, columns=iris.feature_names)
ax = sns.heatmap(df, annot=True, center=0, vmin=-3, vmax=3)
../_images/basic_statistic_values_15_0.png

相関係数

共分散は、もとの値の大きさで数値が決まるので、単位が違う変数を複数比較するときなどに解釈が難しい。たとえば市町村単位で、その町ごとの人口と、ラーメン店の売上の共分散を計算しても、数字の意味がわかりにくい。

そこで関係を見る場合には相関係数を使うことが一般的である。

共分散の値を、各変数の標準偏差の積で割ったものが相関係数となる。相関係数は −1 から 1 までの値をとる。1 であれば 2 つの変数の値は完全に同期していることになる。

\[\rho = \frac{\sigma_{X Y}}{\sigma_X\sigma_Y}\]

\(\rho\) は相関係数、X と Y は、それぞれ異なる特徴量を表す。

相関係数は、共分散を標準化したものと言える（単位の影響を受けずにデータの関連性を示す）。

正規分布（ガウス分布、Normal distribution、Gaussian distrubution）

\[f(x)=\frac{1}{\sqrt{2\pi \sigma^2}} \exp \! \left( -\frac{(x-\mu)^2}{2\sigma^2} \right) \quad(x\in \mathbb{R} )\]

  • ガウス分布は、最も一般的な確率密度関数（積分が確率となる関数）である。

  • 平均 \(\mu\) が分布の中心を表し、標準偏差 \(\sigma\) が分布の幅を表す。

  • 正規分布 N(μ, \(\sigma^2\)) からの無作為標本 x を取ると、平均 μ からのずれが ±1σ 以下の範囲に x が含まれる確率は 68.27%、±2σ 以下だと 95.45%、さらに ±3σ だと 99.73% となる。

  • 正規分布は、t分布やF分布といった種々の分布の考え方の基礎になっているだけでなく、実際の統計的推測においても、仮説検定、区間推定など、様々な場面で利用される。

参考：

ガウス分布を人工的に作ってみる

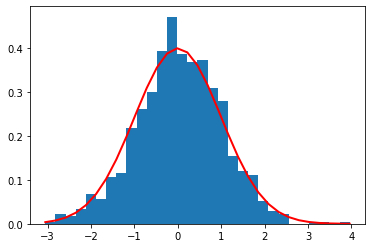
ガウス分布に従ってランダムに生成したデータのヒストグラムと、ガウス分布を重ねて描いたものが以下。

mu が平均値（分布の中心） sigma が標準偏差（分布の幅）

import numpy as np

# ガウス分布に従って乱数生成
mu, sigma = 0, 1 # mean and standard deviatin
np.random.seed(1)
s = np.random.normal(mu, sigma, 1000)

import matplotlib.pyplot as plt

# ヒストグラムの作成
count, bins, ignored = plt.hist(s, 30, density=True)
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *
               np.exp( - (bins - mu)**2 / (2 * sigma**2) ),
         linewidth=2, color='r')
plt.show()
../_images/basic_statistic_values_20_0.png

mu と sigma の値を変えてみて、分布が変わることが確認できる。
また、確率密度関数であるため、横軸の全区間で積分をとると 1 となることが、縦軸の値からイメージできる。

ちなみに、特徴量の尺度を揃えるために行われる標準化では、以下のような処理を行う。

\[ x_{i_{std}} = \frac{x_i-\mu}{\sigma} \]

\( x_{i_{std}} \) : 特徴量 \(x_i\) が標準化されたもの
\( \mu \) : 平均値
\( \sigma \) : 標準偏差

この処理は、平均値を 0、標準偏差が 1 になるように変換している。
つまり、それぞれの特徴量の分布を、正規分布と仮定して、中心が 0、分布の幅が同じスケールのガウス分布に従うように変換していると言える。

この方法は、データを限られた範囲の値にスケーリングする min-max スケーリング（正規化と呼ばれることが多い）とは対照的に、外れ値から受ける影響が少なくなるため、より実用的であると言える。

（正規化、標準化といった言葉は、分野によってはかなり曖昧に用いられることが多く、状況に応じてその意味を推測する必要がある。
また、 \(x_i - \mu\) という操作を mean normalization と呼び、 \(1/\sigma \) することを feature scaling と言ったりする。)

上記は、人工的に作ったガウス分布なので、ヒストグラムと分布が似ているのは当たり前。

ガウス分布を iris データセットにあてはめてみる

今度は自然のデータにガウス関数がうまくフィットするかみたいので、iris データセットを使って確認してみる。

# iris dataset をガウス関数でfittingする

import matplotlib.pyplot as plt

for i_column in iris_df.columns:
  if i_column == 'name':
    continue
  print(i_column)
  mu = iris_df[i_column].mean()
  sigma = iris_df[i_column].std()

  # ヒストグラムの作成
  count, bins, ignored = plt.hist(iris_df[i_column], 30, density=True)
  plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *
                np.exp( - (bins - mu)**2 / (2 * sigma**2) ),
          linewidth=2, color='r')
  plt.show()

sepal length (cm)
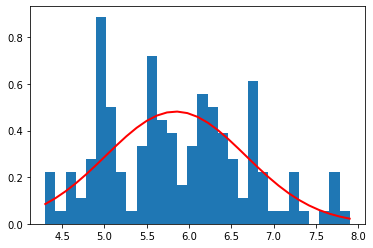
../_images/basic_statistic_values_23_1.png 
sepal width (cm)
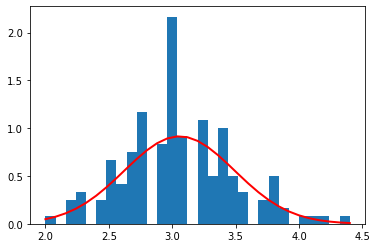
../_images/basic_statistic_values_23_3.png 
petal length (cm)
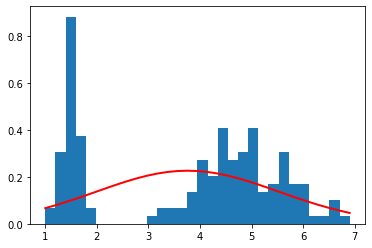
../_images/basic_statistic_values_23_5.png 
petal width (cm)
../_images/basic_statistic_values_23_7.png

Sepal width のみ、かろうじてガウス分布になっている気がするが、その他特徴量はガウス分布になっていないことがわかる。
以上の結果から、iris データセット全体を見ると、ガウス分布は、その分布を表すために適していないように見える。

これは、データセットの中に複数のグループ（iris の種別）のデータが混在しているためであると考えられるため、それぞれのラベル（setosa、versicolor、virginica）ごとにガウス分布を描いてみる。

ラベル（iris の種別）ごとにガウス分布を描いてみる

# 種別ごとに分布を見てみる

for i_name in iris_df['name'].unique():
  print(i_name)
  df_tmp = iris_df[iris_df['name'] == i_name]
  print(df_tmp.shape)

  for i_column in df_tmp.columns:
    if i_column == 'name':
      continue
    print(i_column)
    mu = df_tmp[i_column].mean()
    sigma = df_tmp[i_column].std()

    # ヒストグラムの作成
    count, bins, ignored = plt.hist(df_tmp[i_column], 10, density=True)
    plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *
                  np.exp( - (bins - mu)**2 / (2 * sigma**2) ),
            linewidth=2, color='r')
    plt.show()

setosa
(50, 5)
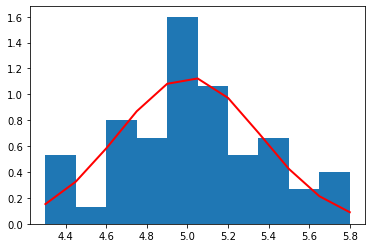
sepal length (cm)
../_images/basic_statistic_values_25_1.png 
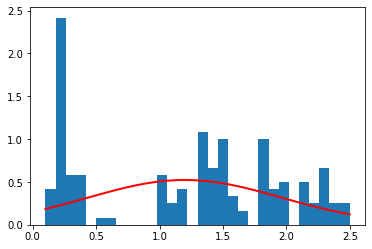
sepal width (cm)
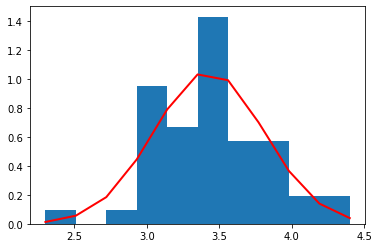
../_images/basic_statistic_values_25_3.png 
petal length (cm)
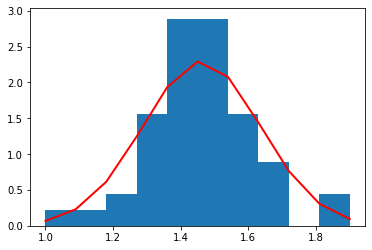
../_images/basic_statistic_values_25_5.png 
petal width (cm)
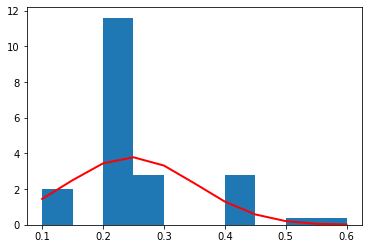
../_images/basic_statistic_values_25_7.png 
versicolor
(50, 5)
sepal length (cm)
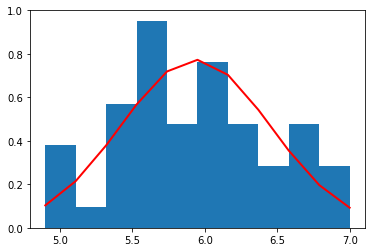
../_images/basic_statistic_values_25_9.png 
sepal width (cm)
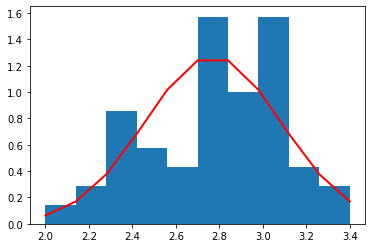
../_images/basic_statistic_values_25_11.png 
petal length (cm)
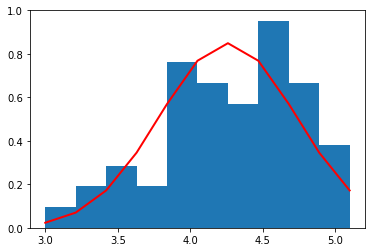
../_images/basic_statistic_values_25_13.png 
petal width (cm)
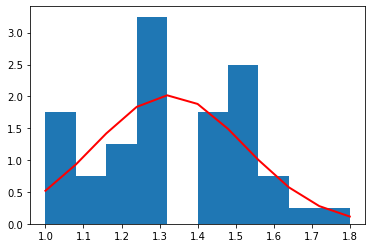
../_images/basic_statistic_values_25_15.png 
virginica
(50, 5)
sepal length (cm)
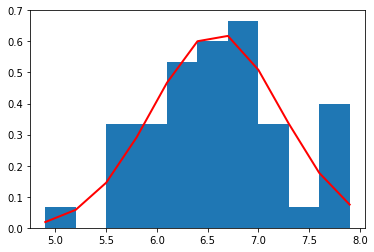
../_images/basic_statistic_values_25_17.png 
sepal width (cm)
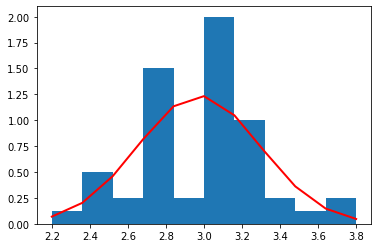
../_images/basic_statistic_values_25_19.png 
petal length (cm)
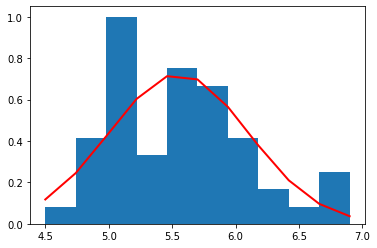
../_images/basic_statistic_values_25_21.png 
petal width (cm)
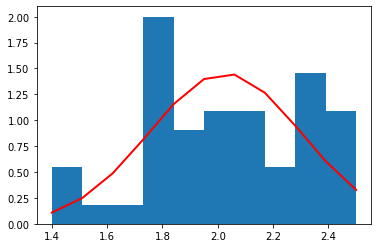
../_images/basic_statistic_values_25_23.png

それぞれの種別ごとのデータ量が少ないため（50個）、ヒストグラムを作るときの bin （集計を取る区切り）の数を 10 個と粗くした。

それぞれの種別ごとに見た場合、すべての特徴量の分布は、ガウス分布によっておおよそ表すことができていることがわかる。

これら、それぞれの種別ごと、特徴量ごとのガウス分布は、平均値と標準偏差によって規定される。
こうして得られたガウス分布により、未知の特徴量のセットに対して、確率を得ることができるので分類器として使うことも可能である（異常検知を話すときに説明したい）。

参考

1

西岡康夫,数学チュートリアル やさしく語る 確率統計,オーム社, p.5, p.52013, ISBN 9784274214073

データ分析 主成分分析 （主成分解析、Principal component analysis : PCA）